Building a Synthesizer, 6

The Logic Circuits Model of Computation

I’m going to step aside from circuit building to talk about the logic circuits model of computation. This may surprise you, reader, as it would at first seem to have nothing to do with building an analog synthesizer. I have a few reasons for doing so. One is that I’ll be talking about analog computers in a future post, so think of this post as a gentle introduction to the topic of alternative computing models. The second is that we can see a synthesizer, whether digital or analog, as a dedicated piece of hardware which can solve a restricted set of computing problems (producing sounds), and I find it interesting to look at a synth from a computing point of view. But analog synthesizers, anyway, are not engineered like most computers!

If you’re strictly interested in synthesis or electrical engineering, then you might want to skip ahead to the next chapter, but if you’re reading my blog then you migth find the following interesting!

Von Neumann Machines

One model of computation, which we’re all very familar with, though perhaps not by this name, is the Von Neumann machine. You are reading this post on a Von Neumann machine right now. It’s so common that we generally just call it a “computer.” Nearly all “computers” produced today are Von Neumann machines, because they are digital computers with a processor, a control unit, memory, mass storage, and I/O. But other computing architectures are possible, and occasionally even useful!

Turing Machines

As a kind of a mental warm-up, consider the Turing machine. The Turing machine was invented years before the Von Neumann machine, and it was not intended to be constructed. Rather, it was a system for modeling computations which we might otherwise think about in our heads. It uses a different system for computation (see the link for details), without memory or random-access storage, but it’s provably equivalent to Von Neumann machines in terms of its computing capabilities. So in this case we have two different models of computation which can solve the same problems, at least if you ignore performance.

Logic Circuits

Another model, which used to be somewhat common, but is far less so given that powerful CPUs can be had for pennies these days, is the logic circuits model. In this case instead of a CPU with an instruction pointer which goes through a list of instructions, fetches data from memory, operates on that data, saves it back to memory, etc., we have a far simpler device which is just a bunch of logic gates. This is so simple, in fact, that it can be efficiently simulated on a Von Neumann machine, so we can either build a logic circuit from raw gates or we can simulate it on a general purpose computer; the result of the computation will be the same either way.

An Example Circuit

Having said that, it’s still an interesting model, and it still has applications today. So let’s give a quick example. Consider the following function in TypeScript:

function doTheThing(a: boolean, b: boolean, c: boolean): boolean {
    if (c) {
        return a && b;
    } else {
        return a || b;
    }
}

This function is of questionable utility, but will serve as a simple example which we can easily translate to a circuits model. It uses a control boolean, c to decide whether to do a boolean AND operation or an OR operation on its other two inputs.

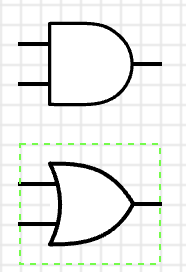
What would a circuits model of this function look like? Well, we have AND and OR as fundamental operators in a circuit, so we can just use those:

So far, so good, but how do we handle the if/then logic? One way is to compute both values, and then decide on which one to use based on the c value:

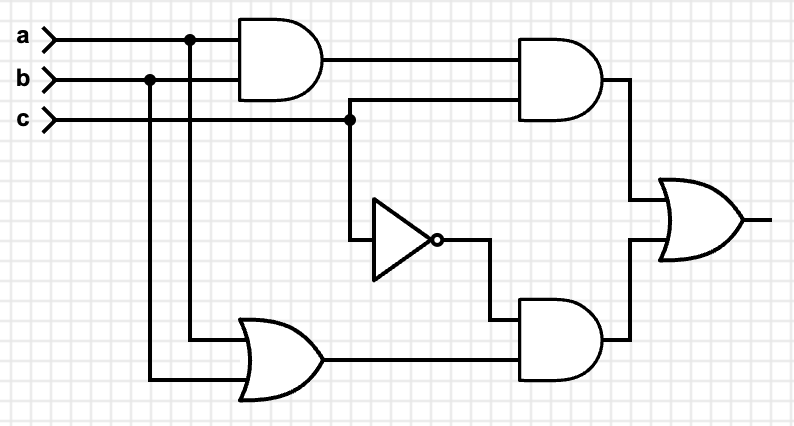
Progress! We have a working circuit. From left to right, we compute both the AND and ORed values, then look at c. We put it directly into one AND gate, and also into another AND gate after first passing it through a NOT gate. Finally we take the OR of both AND gates to see if the output should be high/on/true.

We can prove this works via the following truth table:

a	b	c	output
F	F	F	F
T	F	F	T
F	T	F	T
T	T	F	T
F	F	T	F
T	F	T	F
F	T	T	F
T	T	T	T

You can take a moment and work through the truth table for both the original TypeScript code and the circuit above to prove that they’re the same in all cases. We could leave it at that and be done with it, but looking at the truth table we can see that a somewhat simpler circuit would do:

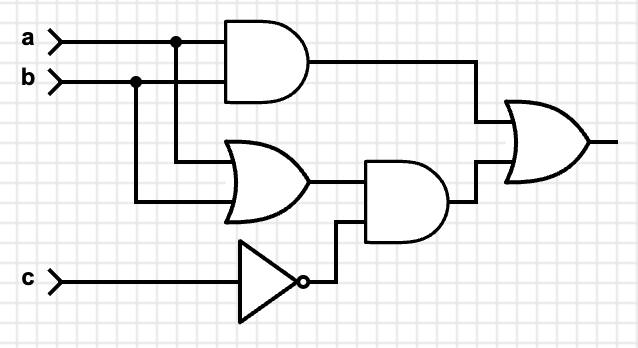
This circuit uses only five gates, instead of six in the original. If you like, you can take a second to convince yourself that the circuit above returns the same values as the truth table, the first circuit, and the TypeScript code. They’re all equivalent.

So even though it might seem inefficient to compute both branches of the if and then pick one, appearances can be deceiving. In general, I worry far more about whether my programs are correct than I do if they are performing as fast as possible (but possibly returning an incorrect result!). If you do need to optimize some routine, it is important to compare the optimized versions in a profiler, not just squint at the code.

Applications of the Logic Circuits Model

This is sort of intellectually interesting, but is there any point in the equivalences above? Why would we bother doing this when general-purpose CPUs are so cheap? It would literally cost more to build a non-trivial circuit with distinct gates than it would to build it on an Arduino or similar, so why am I bothering explaining all of this?

Aside from, you know, building logic circuits, which is sometimes a thing that people do, there are a few cases I can think of where thinking in this model is directly useful:

Compiler Optimizations

If you’re writing a compiler optimizer, you might directly use boolean equivalences such as DeMorgan’s laws to rewrite expressions into other expressions which are guaranteed to return the same result.

GPU Programming

In GPU programming, you often need to write branch-free code whenever possible. Note that the circuits model in the above example was branch-free, whereas the if/then in the TypeScript code was a branch.

Homomorphic Encryption

Homomorphic encryption refers to performing a computation on encrypted data, resulting in the cyphertext of the result of the computation, without ever decrypting the data. It sounds impossible, but turns out to be merely very difficult. With a little thought you will see that if you can’t decrypt the data, then you can’t do a conditinal branch based on some intermediate value (because that would require you to know what the value is, and you don’t; it’s encrypted).

So homomorphic encryption systems often use a logic circuits model of computation, which can be branch free, as shown above. In particular, Craig Gentry’s 2010 thesis, which introduced the first fully homomorphic cryptosystem, used this model.

Mental Exercise

My real agenda here is to get you thinking about different kinds of computing models, because next we’re going to talk about analog computers, and they’re far weirder than logic circuits!

In the next post in this series I’ll building the Mixer module.

References

• Models of Computation: Exploring the Power of Computing, chapter 2: Logic Circuits, Savage, John E., Addison-Wesley, 1998